Critical Temperature Critical Pressure Critical Volume and their Determination
THE CRITICAL PHENOMENON
• According to kinetic theory of gases, the gas molecules are constantly moving. ∴ the gas molecules possess kinetic energy.
• average kinetic energy of the molecules is directly proportional to the absolute temperature.
• Average K.E \(\propto\) absolute temperature.
i.e., As the temperature decreases, the kinetic energy of the molecules also decreases.
As a result, the molecules move closer to each other and the intermolecular forces of attraction increases.
If the process of lowering the temperature is continued, the intermolecular forces of attraction increases so much that the gas converts into liquid, i.e., the liquefaction takes place.
At a given temperature, the gas can also be liquefied by increasing the pressure.
• The increase of pressure also brings the gas molecules closer to one another and ultimately the gas liquefies.
Thus, all gases can be converted into liquids at sufficiently low temperatures and high pressures.
In the process of liquefaction, the effect of temperature is rather more important than that of pressure.
• All gases can be liquefied by lowering the temperature at atmospheric pressure,
• but it is not possible to liquefy all the gases at room temperature by increasing the pressure.
There is an interesting observation that a gas does not liquefy above a certain characteristic temperature, howsoever high may be the pressure. This temperature is called critical temperature of the gas.
Definitions of Critical temperature Critical Pressure and Critical Volume:
Critical Temperature \((T_{C})\) :
• It defined as that temperature above which a gas cannot be liquefied howsoever high pressure may be applied to it.
Critical Pressure \((P_{C})\) :
• The minimum pressure which is just sufficient to liquefy the gas at the critical temperature is called as the critical pressure
Critical Volume \((V_{C})\) :
• It is defined as the volume occupied by one mole of a gas at critical temperature and critical pressure.
T, P and V are called critical constants of the gas.
Note :
• \(V_{c}\), depends to a large extent on the size of the molecule, i.e., Larger the size of the molecule of the substance, larger is its \(V_{c}\)
Experimental Determination of Critical Constants
The determination of critical constants of a gas is based on the fact that at critical temperature and pressure, the physical properties of a gas are indistinguishable from its liquid state and there is no distinction between the two phases.
• At this condition, the densities of liquid and vapour become identical and the surface of separation between them disappears.
Determination of Critical temperature and Critical Pressure
In 1822, Cagniard de La Jour was the first who proposed a method for measurement of critical temperature and critical pressure.
This method was based on the principle that when a liquid is heated in a closed vessel, at a particular temperature, the boundary of separation between the liquid and the vapours disappears. This temperature is called critical temperature.
It may be noted that when these vapours are cooled, the boundary of separation between vapours and liquid reappears at the same temperature i.e. at critical temperature.
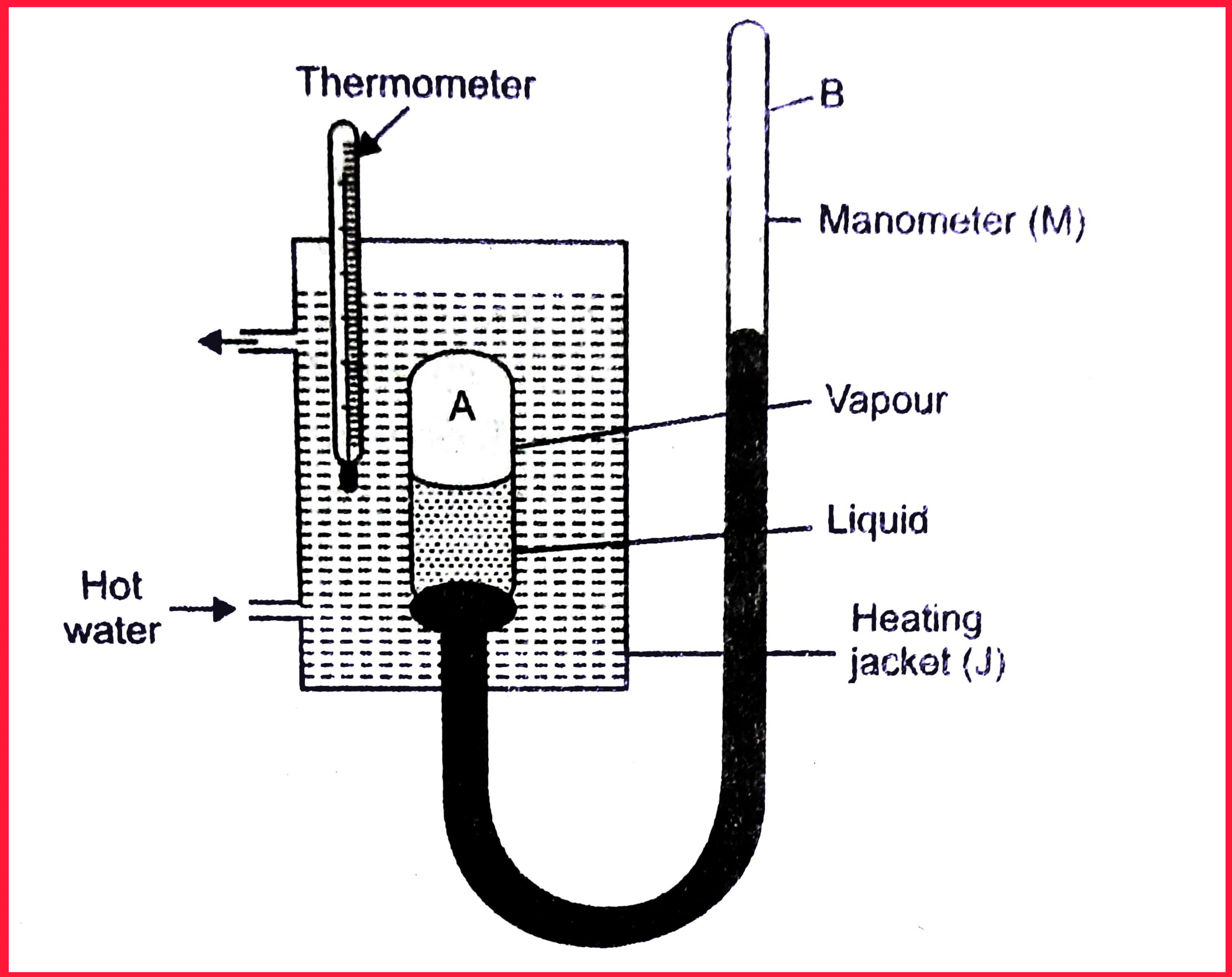
Fig. Caignard de La Tour’s apparatus for determination of Critical temperature and Critical Pressure
The apparatus used for measurement of critical temperature and pressure are as shown in the fig.
- It consists of a strong glass tube A containing the liquid and its vapour enclosed over mercury.
- The bulb A is attached to a mercury manometer M. The bulb A is surrounded by a heating jacket J.
The liquid in the bulb A is gradually heated in the heating jacket until the boundary between the gas and liquid just disappears.
The bulb is then allowed to cool till the meniscus reappears due to condensation of vapour.
The mean of the two temperatures gives the critical temperature \(T_{c}\) of the liquid.
The pressure in the manometer is recorded at both the stages i.e. when the surface of separation disappears on heating and it reappears on cooling the liquid.
The mean of these two pressures gives the critical pressure \(P_{c}\)
Determination of Critical Volume
Experimentally ,the critical volume \(V_{c}\) of the gas cannot be determined because slight changes in pressure and temperature of the gas produce large changes in volume.
•Thus, critical volume is determined indirectly with the help of the rule given by Cailletet and Mathias.
• This rule states that the mean value of the densities of liquid and saturated vapour of any substance at the same temperature is a linear function of the temperature.
To determine the critical volume of a substance, the densities of the liquid \(d_{l}\) and of the saturated vapour \(d_{v}\) in equilibrium with it are plotted against temperatures as shown below in the fig.

Fig. Determination of Critical density & Volume
From graph, it can be seen that :
- the density of vapours increases along the curve AC with increase in temperature ( \(\because\) the vapour pressure is higher at higher temperature)
- while the density of the liquid decreases along curve BC with increase in temperature.
- When these two curves(AC & BC) are extended, they meet at critical temperature \(\because\) at critical temperature the density of liquid and vapour becomes identical.
- The mean values of the densities \((d_{l} + d_{v})/2\) are then plotted against the various temperatures and we obtain a straight line DC as shown in the fig.
- This line passes through the critical temperature viz., given by the point C where the line DC will cut the curve AB.
- The density corresponding to the point C in the graph is the critical density.
- And we can obtain the critical volume by dividing the molecular mass of the liquid by the critical density.

